系统分析与控制小抄
这是我的系统分析与控制期末小抄,是对老师课件的总结。原文由$\LaTeX$编写,可点击此处下载。
Laplace变换
傅里叶变换的定义:$F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt$。绝对可积是充分不必要条件。
拉普拉斯变换的定义:$F(s)=\int_0^{+\infty}f(t)e^{-st}dt$;记号:$F(s)=\mathrm{L}[f(t)],f(t)=\mathrm{L}^{-1}[F(s)]$。
常见函数的拉普拉斯变换:阶跃函数,$f(t)=A,F(s)=\frac{A}{s}$;斜坡函数,$f(t)=At,F(s)=\frac{A}{s^2}$;指数函数,$f(t)=e^{-at},F(s)=\frac{1}{s+a}$;正弦函数,$f(t)=\sin(\omega t),F(s)=\frac{\omega}{s^2+\omega^2}$。
拉普拉斯变换的性质:线性性质,$\mathrm{L}[af_1(t)+bf_2(t)]=aF_1(s)+bF_2(s)$;微分性质,若$f(0)=f’(0)=\cdots=0$,则$\mathrm{L}[f^{(n)}(t)]=s^nF(s)$,否则$\mathrm{L}[f’(t)]=sF(s)-f(0)$;积分性质,$\mathrm{L}[\int_0^tf(\tau)d\tau]=\frac{1}{s}F(s)$;延迟性质,$\mathrm{L}[f(t-\tau)]=e^{-\tau s}F(s)$;终值定理:$\lim\limits_{t\to\infty}f(t)=\lim\limits_{s\to 0}sF(s)$;初值定理:$\lim\limits_{t\to 0}f(t)=\lim\limits_{s\to\infty}sF(s)$。
有理函数的分解:对于$F(s)=\frac{\cdots}{(s-s_1)(s-s_2)\cdots(s-s_n)}$,1) 均为单实根,令$F(s)=\frac{c_1}{s-s_1}+\frac{c_2}{s-s_2}+\cdots+\frac{c_n}{s-s_n}$,则$c_i=\lim\limits_{s\to s_i}(s-s_i)F(s)$,2) 多重实根,令$F(s)=\frac{c_n}{(s-s_1)^n}+\frac{c_{n-1}}{(s-s_1)^{n-1}}+\cdots+\frac{c_1}{s-s_1}$,则$c_n=\lim\limits_{s\to s_1}(s-s_1)^nF(s),c_{n-j}=\frac{1}{j!}\lim\limits{s\to s_1}\frac{d^j}{ds^j}[(s-s_1)^nF(s)]$。
商的求导法则,$[\frac{u}{v}]’=\frac{u’v-uv’}{v^2}$,$[\frac{1}{x}]=-\frac{1}{x^2}$。
时域分析
稳定性
定义:系统偏离平衡状态后,在没有外力作用下,其状态能自动地回到平衡状态。令$y_t(t)$为暂态分量,稳定则$\lim\limits_{t\to\infty}y_t(t)=0$。为什么需要稳定性? 由系统内在特性造成的输出响应必须逐渐衰减并最终消失,从而才可能专心地跟踪输入信号或者抑制干扰影响。
稳定性分析:特征方程的根,1) 都在左半平面,则稳定,2) 虚轴上有单根,其他根都在左半平面,则临界稳定,3) 由半平面有根或者虚轴上有重根,则不稳定。
传递函数:零初始条件。$G(s)=\frac{Y(s)}{R(s)}$,其中$Y(s)$是输出,$R(s)$是输入。特征方程的根就是传递函数的极点。
结构图
闭环传递函数:令$G(s)$是前向传递函数,$H(s)$是负反馈传递函数,则闭环传递函数$\frac{Y(s)}{R(s)}-\frac{G(s)}{1+G(s)H(s)}$。
结构图的等效与化简:略。
劳斯判据(根稳定性判别方法):对于6次方程$F(s)=a_0s^6+a_1s^5+\cdots+a_5s+a_6$,如下列出前两行:
|-|-|-|-|-| | $s^6$ | $a_0$ | $a_2$ | $a_4$ | $a_6$ | | $s^5$ | $a_1$ | $a_3$ | $a_5$ | 0 |
然后按照$a_{ij}=-\frac{1}{a_{i-1,1}}\begin{vmatrix} a_{i-2,1} & a_{i-2,j+1} \ a_{i-1,1} & a_{i-1,j+1} \end{vmatrix}$,填充其它行。第一列符号改变次数等于右半平面根数。若劳斯判据第一列无符号改变,则根稳定。
劳斯判据第一列为0:如果某一行第一个元素为0,其余元素不为0,将0代替为一个小的正数$\epsilon$;如果某一行第一个元素为0,其余元素也为0,则有关于原点对称的根,这时使用辅助多项式,求其微分作为新的一行,例子如下。
|-|-|-| | $s^3$ | 6 | 6 | | $s^2$ | 4 | 4 | | $s^1$ | 0 | 0 |
这时辅助多项式为$A(s)=4s^2+4$,则$\frac{dA(s)}{ds}=8s$,故最后的表格如下。
|-|-|-| | $s^3$ | 6 | 6 | | $s^2$ | 4 | 4 | | $s^1$ | 8 | 0 | | $s^0$ | 4 | |
稳态性能
产生原因:反馈控制系统需要误差信号来产生控制作用。如果稳态时仍然需要控制作用,就必须有非零的误差以维持控制作用($u=Ke$)。从而产生了稳态误差。
计算稳态误差的前提:系统是稳定的。
输入稳态误差和干扰稳态误差计算如下。

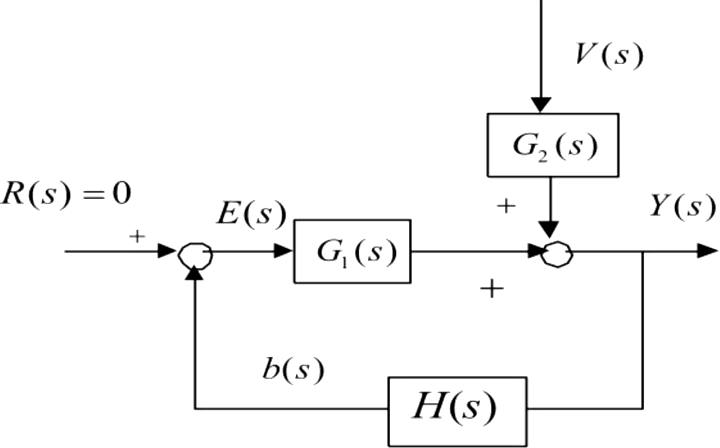
$$e_{ss}=\lim_{s\to 0}\frac{sR(s)}{1+G_1(s)H(s)}+\lim_{s\to 0}\frac{-sG_2(s)H(s)V(s)}{1+G_1(s)H(s)}$$
阶跃输入下的稳态误差:$e_s=\frac{R}{1+\lim\limits_{s\to 0}G_1(s)H(s)}=\frac{R}{1+K_p}$,其中$K_p=\lim\limits_{s\to 0}G_1(s)H(s)$为位置品质系数。
斜坡输入下的稳态误差:$e_s=\frac{R}{\lim\limits_{s\to 0}sG_1(s)H(s)}=\frac{R}{K_v}$,其中$K_v=\lim\limits_{s\to 0}sG_1(s)H(s)$为速度品质系数。
斜坡输入下的稳态误差:$e_s=\frac{R}{\lim\limits_{s\to 0}s^2G_1(s)H(s)}=\frac{R}{K_a}$,其中$K_a=\lim\limits_{s\to 0}s^2G_1(s)H(s)$为加速度品质系数。
稳态误差总结:令 $$G_1(s)H(s)=\frac{K\prod\limits_{k=1}^p(T_ks+1)\prod\limits_{l=1}^q(T_l^2s^2+2\xi_lT_ls+1)}{s^r\prod\limits_{i=1}^m(T_is+1)\prod\limits_{j=1}^n(T_j^2s^2+2\xi_jT_js+1)}$$
| 阶跃 | 斜坡 | 抛物线 | |
|---|---|---|---|
| $r=0$ | $\frac{R}{1+K}$ | $\infty$ | $\infty$ |
| $r=1$ | $0$ | $\frac{R}{K}$ | $\infty$ |
| $r=2$ | $0$ | $0$ | $\frac{R}{K}$ |
$\frac{1}{s}$越多,稳态性能越好。
动态性能
超调量:$\sigma=\frac{y_m-y_s}{y_s}$,其中$y_s$是稳态值不是期望值。
过渡过程时间:$t_s$是进入稳态值5%范围的时间。
一阶系统定量分析:传递函数为$\frac{1}{Ts+1}$。单位阶跃响应为$y(t)=1-e^{-t/T}$。$\sigma=0,t_s\approx 3T$。
二阶系统定量分析:传递函数为$\frac{\omega^2}{s^2+2\xi\omega s+\omega^2}$。$\xi>0$则稳定。 $$\sigma=\begin{cases} 0 & \xi\geq 1 \ e^{-\frac{\pi\xi}{\sqrt{1-\xi^2}}} & 0<\xi<1 \end{cases}$$ $$t_s\begin{cases} \frac{3.2}{\xi\omega} & 0<\xi<0.69 \ \frac{2.8+6.5(\xi-0.7)}{\omega} & \xi\geq 0.69 \end{cases}$$
高阶系统的近似简化:设传递函数为$M(s)=\frac{K(s-z_1)\cdots(s-z_m)}{(s-p_1)\cdots(s-p_n)}$,1) 零极点相消,$|p_k-z_r|$很小时对消,结果为$\bar{M}(s)=\frac{Kz_r}{p_k}\frac{\prod\limits_{j=1,k\neq r}^m(s-z_j)}{\prod\limits_{i=1,i\neq k}^n(s-p_i)}$,右半平面的零、极点不能对消;2) 远极点消除,对于$\mathrm{Re}(p_k)$很小的情况,可消除该极点,结果为$\bar{M}(s)=\frac{K}{p_k}\frac{\prod\limits_{j=1}^m(s-z_j)}{\prod\limits_{i=1,i\neq k}^n(s-p_i)}$。消除时稳态放大倍数应不变。
状态方程
状态方程的一般形式: $$\begin{cases} \dot{x}(t)=Ax(t)+Bu(t) \ y(t)=Cx(t)+Du(t) \end{cases}$$
状态方程之间的转换:状态变量的选取不唯一,从而状态方程不唯一(传递函数是唯一的)。如果$\bar{x}(t)=Px(t)$,则新状态方程的各个参数变为$\bar{A}=PAP^{-1},\bar{B}=PB,\bar{C}=CP^{-1},\bar{D}=D$。
状态方程到传递函数的转换:初态必须是0,即$x(0)=0$,此时$G(s)=C(sI-A)^{-1}B+D$;否则$Y(s)=G(s)U(s)+Cx(0)$。
传递函数到状态方程的转换:设$G(s)=\frac{Y(s)}{U(s)}=\frac{b_0s^m+b_1s^{m-1+\cdots+b_{m-1}s+b_m}}{s^n+a_1s^{n-1}+\cdots+a_{n-1}s+a_n}$。若$n>m$,则 $$A=\begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \ 0 & 0 & 1 & \cdots & 0 \ \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & 0 & \cdots & 1 \ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{bmatrix} B=\begin{bmatrix} 0 \ 0 \ \vdots \ 0 \ 1 \end{bmatrix}$$ $$ C = \begin{bmatrix} b_m & b_{m-1} & \cdots & b_1 & b_0 & 0 & \cdots & 0 \end{bmatrix}, D = 0 $$ 若$n=m$,则$D=b_0$。
非线性系统的线性化:
$$\begin{align*} \frac{dx(t)}{dt}=f(x,u)\approx f(x_0,u_0)&+\frac{\partial f(x,u)}{\partial x}\bigg\rvert_{(x_0,u_0)}(x-x_0) \ &+\frac{\partial f(x,u)}{\partial u}\bigg\rvert_{(x_0,u_0)}(u-u_0) \end{align*}$$
选择工作点$f(x_0,u_0)=0$,令$\tilde{x}=x-x_0, \tilde{u}=u-u_0$。
步骤:
- 列写原始微分方程
- 建立状态方程
- 确定工作点
- 建立增量的线性化方程
频域分析
频域分析的特点:稳定的线性系统不改变输入正弦信号的频率,只改变输入正弦信号的幅值和相位。
与时域响应的关系:将传递函数中的$s$替换为$j\omega$即可得到频率特性。
一阶系统的频率特性:$G(j\omega)=\frac{1}{j\omega T+1}$,故幅频$A(\omega)=|G(j\omega)|=\frac{1}{\sqrt{(\omega T)^2+1}}$,相频$\angle G(j\omega)=-\arctan(\omega T)$。可以看出:1) 低频信号,幅值衰减少,相位偏移少,能够基本复现输入信号;高频信号,幅值衰减很多,相位偏移很大,信号变形很厉害。2) 定义$\omega_b=\frac{1}{T}$,它是输出下降到$0.707A$处的频率,$\omega_b$大则可通过的频率成分越多,惯性小,输出过渡过程也越快;$\omega_b$小则惯性大。
极坐标图:$G(j\omega)=A(\omega)e^{j\varphi(\omega)}$,作出极坐标的参数方程。
Bode图:横坐标采用10倍频程$\log(\omega)$。上方是幅频图,纵坐标$L(\omega)=20\log(A(\omega))$。下方是相频图。
一阶系统的Bode图:1) $\omega T\ll 1$,则$A(\omega)\approx 1,L(\omega)\approx 0,\varphi(\omega)\approx 0$;2) $\omega T\gg 1$,则$A(\omega)\approx\frac{1}{\omega T},L(\omega)\approx 20\log(\frac{1}{T})-20\log{\omega},\varphi(\omega)\approx -90^{\circ}$,3) $\omega T=1$,则$A(\omega)=\frac{1}{\sqrt{2}},L(\omega)\approx -3,\varphi(\omega)=-45^{\circ}$。
Bode图的性质:
- 采用频率的对数坐标,展宽了视野
- 作图容易,可利用折线段近似
- 频率特性乘除对应于幅频特性曲线加减
- 频率特性的纵向放大、缩小对应于幅频特性曲线的上移和下移
- 简化了频率特性的倒数关系
基本环节的Bode图:1) 比例环节$G(s)=K$,则$L(\omega)=20\log(k),\varphi(\omega)=0$;2) 积分环节$G(s)=\frac{1}{s}$,则$L(\omega)=-20\log\omega,\varphi(\omega)=-90^{\circ}$;3) 微分环节$G(s)=s$,则$L(\omega)=20\log\omega,\varphi(\omega)=90^{\circ}$。
二阶震荡环节的Bode:$G(s)=\frac{1}{T^2s^2+2\xi Ts+1}, 0\leq \xi<1$,$G(j\omega)=\frac{1}{1-\omega^2T^2+2\xi\omega Tj}$,则 $$A(\omega)=\frac{1}{\sqrt{(1-\omega^2T^2)^2+(2\xi\omega T)^2}}$$ $$\varphi(\omega)=-\arctan\frac{2\xi\omega T}{1-\omega^2T^2}$$ $$L(\omega)=-20\log\sqrt{(1-\omega^2T^2)^2+(2\xi\omega T)^2}$$
- $\omega\ll\frac{1}{T}$,则$L(\omega)\approx 0,\varphi(\omega)\approx 0$;2) $\omega\gg\frac{1}{T}$,则$L(\omega)\approx 20\log\frac{1}{(\omega T)^2}=40\log\frac{1}{T}-40\log\omega,\varphi(\omega)\approx-180^{\circ}$;3) $\omega=\frac{1}{T}$,则$L(\omega)=-20\log(2\xi),\varphi(\omega)=-90^{\circ}$。
一般传递函数的Bode图:一般地,$G(s)=G_1(s)G_2(s)\cdots G_n(s)$,则$L(\omega)=L_1(\omega)+L_2(\omega)+\cdots+L_n(\omega)$,$\varphi(\omega)=\varphi_1(\omega)+\varphi_2(\omega)+\cdots+\varphi_n(\omega)$。对下方的传递函数: $$G(s)=\frac{K\prod\limits_{k=1}^p(T_ks+1)\prod\limits_{l=1}^q(T_l^2s^2+2\xi_lT_ls+1)}{s^r\prod\limits_{i=1}^m(T_is+1)\prod\limits_{j=1}^n(T_j^2s^2+2\xi_jT_js+1)}$$
幅频特性作图步骤如下:
- 化标准形
- 低频部分:找$\omega=1,L(\omega)=20\log K$的点,由该点向左画斜率为$-20r$的斜线
- 求转折频率$\omega_i=1/T_i$,并由小到大排序,$\omega_1<\omega_2<\cdots$
- 从低频渐近线开始自左向右画,碰到$\omega_i$就拐弯,分母环节向下弯,分子环节向上弯,一阶环节斜率变20,二阶环节变40
- 修正(圆滑过渡)
相频特性作图步骤如下:
- 画$-90^{\circ}\times r$水平线
- 算出转折点$\varphi(\omega)$
- 粗画相频特性$\varphi(\omega)$
稳定裕量:令$\omega_c$为剪切频率,即$L(\omega)=0$时$\omega$的值,则稳定裕量为$\gamma=\varphi(\omega_c)-(-180^{\circ})$。一般而言,$30^{\circ}\leq\gamma\leq 70^{\circ}$是可接受的范围。$\gamma$太小,稳定裕量小,超调大,振荡多;$\gamma$太大,稳定裕量大,动态响应慢,过渡过程时间长。
采样控制系统
概念
采样控制系统的特性:采样周期越小,采样信号越接近原始信号。香农定律:为了完美地重构信号,需要按照不小于2倍带宽采样率对信号进行采样。数学描述:$e^*(t)=\sum\limits_{k=0}^{\infty}e(kT)\delta(t-kT)$。
系统分类:
- 连续控制系统:连续信号
- 离散控制系统:离散信号
- 采样控制系统:连续、离散信号
- 数字控制系统:连续、离散信号,量化效应
采样系统的数学模型: $$\begin{cases} x(k+1)=Fx(k)+Gu(k) \ y(k)=Cx(k)+Du(k) \end{cases}$$
Z变换
Z变换:$R(z)=\sum\limits_{k=0}^{+\infty}r(k)z^{-k}$。
常见Z变换:1) 对于$r(k)=\begin{cases}1 | k=0 \ 0 | k\neq 0\end{cases}$,有$R(z)=1$;2) 对于$r(k)=\begin{cases}1 | k\geq 0 \ 0 | k<0\end{cases}$,有$R(z)=\frac{z}{z-1}$。
Z变换性质:1) 线性性质,$Z[ar_1(t)+br_2(t)]=aR_1(z)+bR_2(z)$;2) 延迟性质,$Z[r(k-1)]=z^{-1}R(z)$;3) 超前性质,$Z[r(k+1)]=z(R(z)-r(0))$;4) 初值定理,$\lim\limits_{k\to 0}r(k)=\lim\limits_{z\to\infty}R(z)$;5) 终值定理,$\lim\limits_{k\to\infty}r(k)=\lim\limits_{z\to 1}(1-z^{-1})R(z)$。
离散与连续之间的转换
连续系统对应的离散化模型: $$F=e^{AT},G=\left(\int_0^Te^{AT}dt\right)B$$
连续传递函数到离散传递函数的转换: $$G(z)=Z\left[\frac{1-e^{-Ts}}{s}G(s)\right]=(1-z^{-1})Z\left[\frac{1}{s}G(s)\right]$$
离散状态方程到传递函数的转换:与连续类似。 $$G(z)=C(zI-F)^{-1}G+D$$
离散传递函数到状态方程的转换:与连续类似。
离散系统稳定性
离散系统稳定性条件:特征方程的根均在单位圆内。先作替换$z=\frac{\omega+1}{\omega-1}$,再用劳斯判据。
离散系统稳态性能
阶跃输入下的稳态误差:输入$R(z)=R\frac{z}{z-1}$,$e_s=\frac{R}{1+\lim\limits_{z\to 1}D(z)G(z)}=\frac{R}{1+K_p}$,其中$K_p=\lim\limits_{z\to 1}D(z)G(z)$为位置品质系数。
斜坡输入下的稳态误差:输入$R(z)=R\frac{Tz}{(z-1)^2}$,$e_s=\frac{R}{\lim\limits_{s\to 1}\frac{z-1}{T}D(z)G(z)}=\frac{R}{K_v}$,其中$K_v=\lim\limits_{z\to 1}\frac{z-1}{T}D(z)G(z)$为速度品质系数。
斜坡输入下的稳态误差:输入$R(z)=R\frac{T^2z(z+1)}{2(z-1)^3}$,$e_s=\frac{R}{\lim\limits_{z\to 1}(\frac{z-1}{T})^2D(z)G(z)}=\frac{R}{K_a}$,其中$K_a=\lim\limits_{z\to 1}(\frac{z-1}{T})^2D(z)G(z)$为加速度品质系数。
总结:
| $\frac{1}{(z-1)^r}$ | 阶跃 | 斜坡 | 抛物线 |
|---|---|---|---|
| $r=0$ | $\frac{R}{1+K_p}$ | $\infty$ | $\infty$ |
| $r=1$ | $0$ | $\frac{R}{K_v}$ | $\infty$ |
| $r=2$ | $0$ | $0$ | $\frac{R}{K_a}$ |
离散系统动态性能
近似等效法 $$z=e^{sT}\approx\frac{1+sT/2}{1-sT/2}$$
现代控制理论
极点配置: 设$u(t)=-Lx(t)$,要适当选取$L$,通过改变$x(t)$的运动规律,间接改变了输出$y(t)$的运动规律。设期望的极点为$p_1,p_2,\cdots,p_n$,则可求解$|sI-(A-BL)|=(s-p_1)(s-p_2)\cdots(s-p_n)$得到$L$。
能控性:$S=\begin{bmatrix} B | AB | \cdots | A^{n-1}B \end{bmatrix}$满秩则能控。